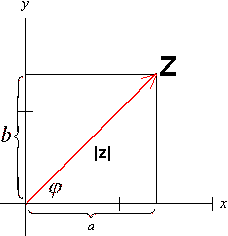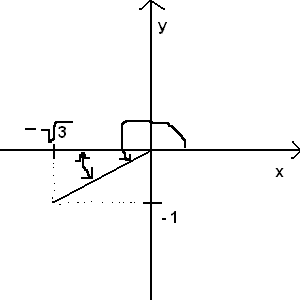|
Definicja pary uporządkowanej:
Para uporządkowana to zbiór zbudowany z dwóch obiektów, a i b w taki sposób, by była określona kolejność tych elementów.
Oznaczenie pary uporządkowanej:
(a,b)
a - poprzednik (pierwszy w kolejności), b - następnik (kolejne)
Definicja zbioru liczb zespolonych:
Zbiorem liczb zespolonych nazywamy zbiór uporządkowanych par liczb rzeczywistych (a,b) w których określone są trzy relacje:
1) relacja tożsamości (a,b)=(c,d) ⇔ (a=c i b=d)
2) działanie dodawania (a,b)+(c,d) = (a+c,b+d)
3) działanie mnożenia (a,b)*(c,d ) = (ac-bd,ad+bc)
liczbą zespoloną nazywamy elementem tego zbióru.
Określenie zbioru liczb zespolonych:
C
UWAGA
Liczbę zespoloną w postaci (a,0) można utożsamiać z liczbą rzeczywistą a:
(a,0) = a
Postać algebraiczna liczby zespolonej
Oznaczenia:
(0,1) = i
i - jednostka urojona
i² = -1
i² = i*i = (0,1)*(0,1) = (0*0-1,0+0) = (-1,0) = -1
dla dowolnej liczby zespolonej z mamy:
z = (a,b) = (a,0)+(0,b) = (a,0)+(b,0)*(0,1) = a+bi
Liczbę a+bi, gdzie a,b∈R nazywamy podstawą algebraiczną (kartezjańską) liczby zespolonej:
a - cześć rzeczywista ℜ (Rez); b - cześć urojona ℑ (Imz)
Przykład:
z=5+2i
ℜ (Rez) = 5
ℑ (Imz) = 2
Działania na liczbach zespolonych w postaci algebraicznej
Dane są liczby z1 = a+bi, z2 = c+di
1) z1+z2 = a+bi,c+di = a+c, bi+di = a+c+(b+d)i
2) z1*z2 = (a+bi)*(c+di) = ac+adi+cbi+bdi² = (a,b)*(c,d) = (ac-bd,ad+bc) = ac-bd+(ad+bc)i
liczby sprzężoną do liczby z = x+yi nazywamy liczbę ¬z = x-yi (¬ - negacja)
3) z1/z2 = z1*¬z2/z2*¬z2 = (a+bi)*(c-di)/(c+di)*(c-di) = ac-adi+bci-bdi²/c²+d² = ac+bd-(ad+bc)i/c²-d²
Przykład:
1) (3-2i)*(2+i) = 6+3i-4i-2i² = 8-i
2) 4+5i/7-i = (4+5i)*(7+i)/(7-i)*(7+i) = 28+4i+35i-5/49+1 = 23+39i/50
Interpretacja geometryczna liczby zespolonej
Niech z = a+bi = (a,b) a,b∈R
liczbę zespoloną interpretujemy jako punkt P=(a,b) w płaszczyźnie Oxy albo jako jako wektor o początku w punkcie O(0,0) i końcu w punkcie P (a,b)

Moduł i orgument liczby zespolonej
Długośc wektora OP nazywamy modułem liczby zespolonej z = a+bi i oznaczamy |z| = (a²+b²)1/2
Kąt ƒ między dodatnią cześcia osi OX (rzeczywistą) a wektorem OP nazywamy argumentem liczby zespolonej z = a+bi ≠0
Oznaczenia:
Argz
UWAGA
Argumentem liczby z = 0, jest każda liczba rzeczywista.
Argument liczby zespolonej nie jest określony jednoznacznie.
Jeśli ƒ jest argumentem liczby zespolonej to równierz ƒ+2π jest argument tej liczby.
Argumentem głównym liczby zespolonej z = ≠0 nazywamy argument tej liczby spełniający warunek 0≤ƒ2π i oznaczamy go argz.
UWAGA
Czasem wygodniej jest przyjąć, że argument główny jest liczbą z przedziału (-π,π)
Przykład:
Wyznaczyć |z| i argz
a) z = -(3)1/2 - i
|z| = {[-(3)1/2]²+(-i)²}1/2
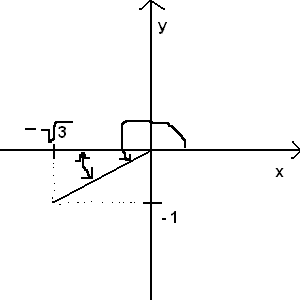
argz = ƒ = π+α
tgα = 1/(3)1/2
α = π/6
argz = π+π/6 = 7/6*π
Postać wykładnicza i trygonometryczna liczby zespolonej
Niech z = a+bi ; a,b∈R
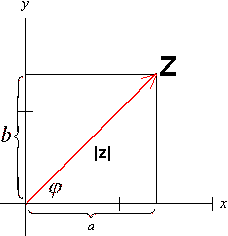
a = |z|cosƒ
b = |z|sinƒ
z = |z|(cosƒ+isinƒ) - postać trygonometryczna
Definicja
Dla ƒ∈R
eiƒ = cosƒ+isinƒ
z = |z|eiƒ - postać wykladnicza
Mnożenie postaci trygonometrycznej
Niech:
z1 = |z1|(cosƒ1+isinƒ1)
z2 = |z2|(cosƒ2+isinƒ2)
z1*z2 = |z1|*|z2|[cosƒ1*cosƒ2-icosƒ1*sinƒ2+isinƒ1*cosƒ2+i²sinƒ1*sinƒ2) = |z1|*|z2|((cosƒ1*cosƒ2-sinƒ1*sinƒ2+i(cosƒ1*sinƒ2+sinƒ1*cosƒ2)] =
|z1|*|z2|[cos(ƒ1+ƒ2)+isin(ƒ1+ƒ2)]
Potęgowanie postaci trygonometrycznej
Niech:
z = |z|(cosƒ+isinƒ)
z² = z*z = |z|²(cos2ƒ+isin2ƒ)
z3 = z*z*z = |z|3(cos3ƒ+isin3ƒ)
zn = |z|n(cosnƒ+isinnƒ) - wzór Moivre'a
Dzielenie postaci trygonometrycznej
Pierwiastki stopnia n∈N z liczby zespolonej z nazywamy taką liczbe zespolonąW, że:
Wn = z
zbiór pierwiastków stopnia n zliczby zespolonej z oznaczamy przez z1/n
Porównanie pierwiastków w dziedzinie rzeczywistej i zespolonej:
liczby rzeczywiste | liczby zespolone |
41/2 = 2 | 41/2 = {2,-2} |
11/4 = 1 | 11/4 = {-1,-i,1,i} |
11/2 = nie istnieje | 11/2 = {i,-i} |
(x2)1/2 = |x| | (x2)1/2 = {x,-x} |
z = |z|(cosƒ+isinƒ)
z1/n = {Wo,W1,...,Wn-1}
Wk = |z|1/n(cos*ƒ+2kπ/n+isin*ƒ+2kπ/n) ; k=0,...,n-1
Mnożenie postaci trygonometrycznej
Niech:
z1 = |z1|eiƒ1
z2 = |z2|eiƒ2
z1*z2 = z1eiƒ1*|z2|eiƒ2 = |z1|*|z2|ei(ƒ1+ƒ2)
Dzielenie postaci trygonometrycznej
Niech:
z1 = |z1|eiƒ1
z2 = |z2|eiƒ2
z1/z2 = z1eiƒ1/|z2|eiƒ2 = |z1|/|z2|ei(ƒ1-ƒ2)
|