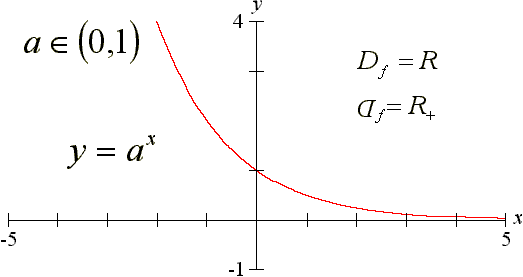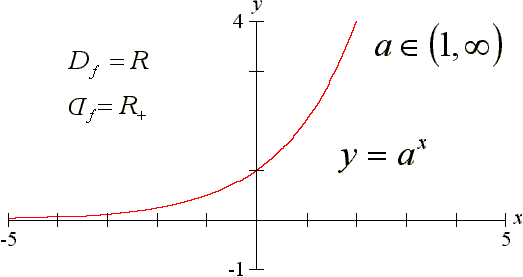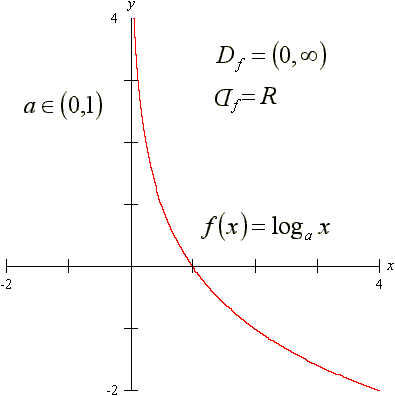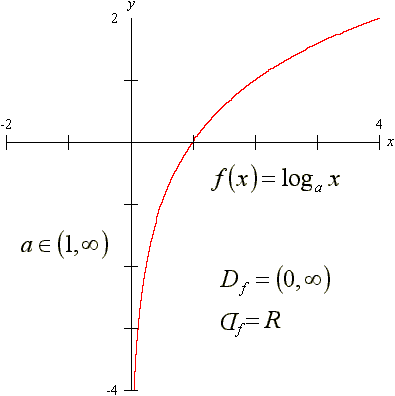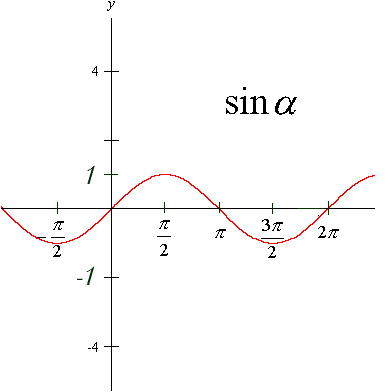Oznaczenia zbiorów liczbowych:
N - zbiór liczb naturalnych
Z - zbiór licz całkowitych
Q - zbiór licz wymiernych
R - zbiór liczb rzeczywistych
C - zbiór licz zespolonych

Oznaczenia znaków logicznych:
∧ - i
∨ - lub
⇒ - z... wynika...
⇔ - wtedy i tylko wtedy gdy
∀ - kwantyfikator duży (ogolny, uniwersalny) - dla każdego
∃ - kwantyfikator mały (szczegółowy) - istnieje takie x, że...

Oznaczenia znaków z teorii zbiorów:
∈ - należy do...
∉ - nie należy do...
⊂ - zawiera się w...
∪ - suma zbiorów
∩ - część wspólna zbiorów
∅ - zbiór pusty

Definicja fukcji:
Funkcja określona na zbiorze x⊂R o wartościach w zbiorze y⊂R, nazywamy przyporządkowanie każdemu elementowi x∈X dokładnie jednego elementu y∈Y.
Zapis ƒ: X→Y czytamy: ƒ jest funkcją odwzorowującą zbiór X w zbiór Y.

Wartość funkcji ƒ w punkcie x oynacyamz ƒ(x)
Pełny zapis funkcji ma postać:
ƒ:X→Y
X→ƒ(x)

Zapisujemy równierz:
X∋x→ƒ(x)∈Y
tradycyjnie
y = ƒ(x) , x∈X

Przykład:
1) ƒ:'R→R
x→x²+3
2)y = x²+3 ; x∈R

Definicja:
Niech dana bedzię funkcja ƒ:X→Y wtedy zbiór X nazywamy dziedziną funkcji i oznaczamy D_ƒ (lub D), zbiór Y nazywamy przeciwdziedziną funkcji.
Zbiór taki {ƒ(x)∈Y , x∈D_ƒ nazywamy zbiorem wartości funkcji ƒ i oznaczamy W_ƒ lub ƒ(x).

Uwaga:
1) W_ƒ⊂Y
2) Jeśli ƒ: x→y spełnia warunek W_ƒ = y to mówimy, że ƒ odwzorowywuje zbiór X na zbiór Y, co symbolicznie zapisujemy: ƒ:X-na->Y

Definicja wykresu funkcji:
Wykresem funkcji ƒ:X→Y nazywamy zbiór par (x,ƒ_k), gdy x∈X

Przykłady funkcji:

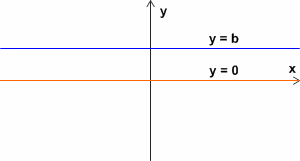
Funkcja stała:
y = a , a∈R (a - parametr)

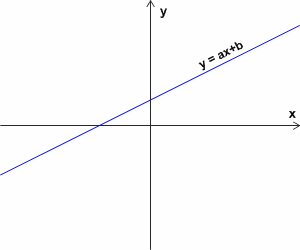
Funkcja liniowa:
y = ax+b , (a i b - parametry)

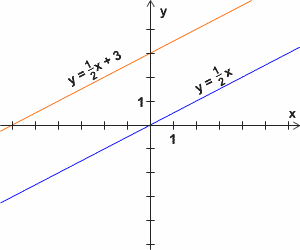
Funkcje liowe dla y = 1/2*x+3 i y = 1/3*x

Funkcja moduł:
y = |x|
|x| = x dla x≥0 (dla nieujemnych) i -x dla x<0 (dla ujemnych)
(x²)^1/2 = |x|

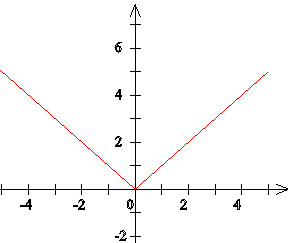
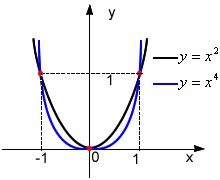
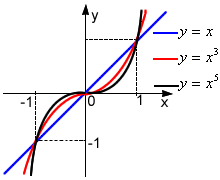
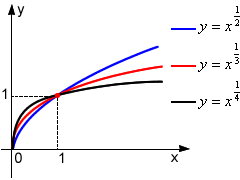
Funkcja potęgowa:
y = x^a ; a∈R (a - jest parametrem)
dziedzina zależy od parametru a
przykłady:

Funkcja wielomianowa (wielomian):
W(z) = a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀
W₁(x) = 4 - funkcja stała
W₂(x) = 5x+7 - funkcja liniowa
W₃(x) = 3x²+7x+2 - funkcja kwadratowa

Funkcja wymierna:
y = P_(x)/Q_(x) , P_(x),Q_(x) - to wielomiany
Dziedzina: D = {x∈R:Q_(x)≠0}
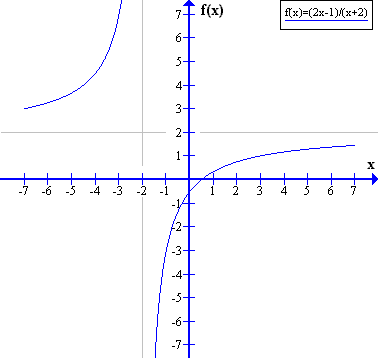
Szczególnym przypadkiem funkcji wymiernej jest funkcja homograficzna y = ax+b/cx+d , c≠0, a²+b²>0 - a,b różne od zera
D = {a∈R; cx+d≠0}
dla y = (2x-1)/(x+2)

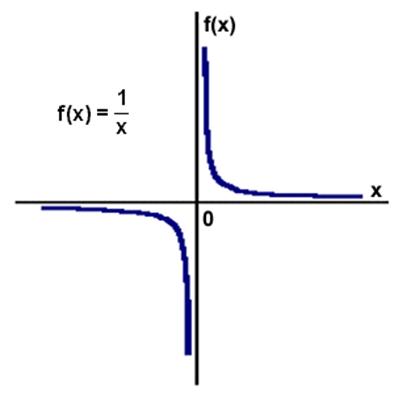
dla y = 1/x
D = {x∈R , x≠0} = (-∞;0)∪(0;+∞)}

Funkcja wykładnicza:
y = a^x , a>0
dla 0<a<1

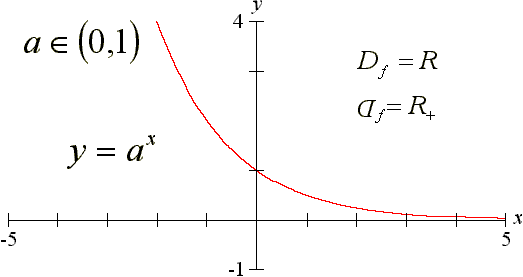
dla a>1

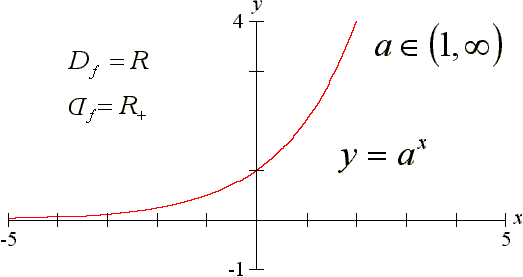
Funkcja logarytmiczna:
Definicja logarytmu:
Jeżeli a>0 i a≠1 to:
log_ab = c ⇔ b = a^c , b>0

Właśności logarytmów:
log_a1 = 0
log_aa = 1
log_ab*c = log_ab+log_ac
log_ab/c = log_ab-log_ac
log_a(b)^p = p*log_ab
log_ab = log_db/log_da
log_aa^y = y
a^log_ax = x , x>0

Przykłady:
3 = log₅5 = 3log₅5 = log₅5³
2,1 = log₂2^2,1
3 = log₂2³
0,5 = log₂2^1/2
2,5 = log₂2^2,5

3^x=4 , a=3, b=4, c=x
x = log₃4
3^x=4
log₃3^x = log₃4
xlog₃3 = log₃4
x = log₃4

Postać graficzna
dla a>0

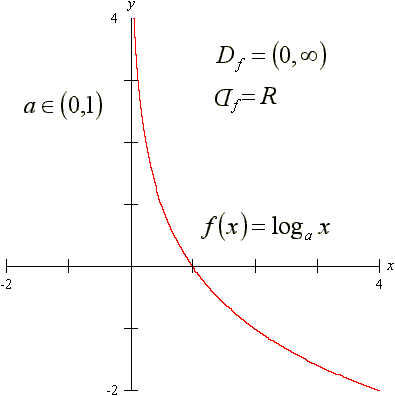
0<a<1

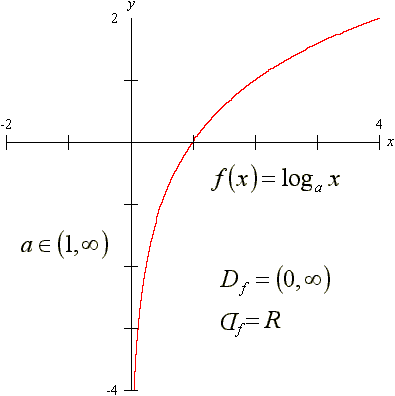
Funkcje trygonometryczne:
y = sinx

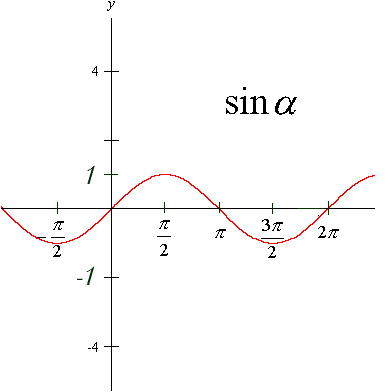
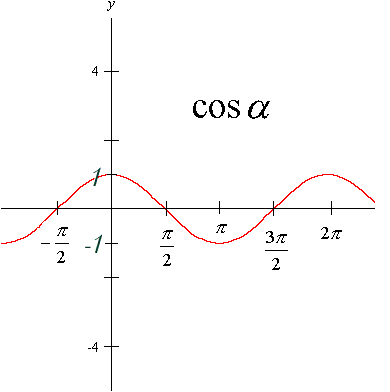
y = cosx

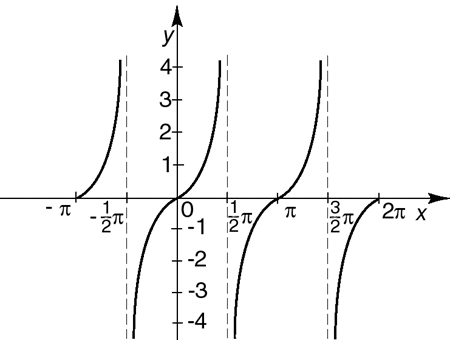
y = tgx D = {x∈R, x≠π/2+kπ, k = Z}

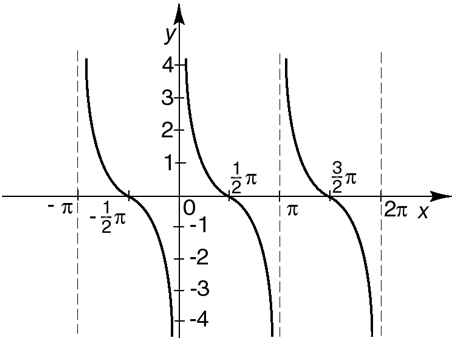
y = ctgx D = {x∈R, x≠kπ, k = Z}

Funkcje hiperboliczne:
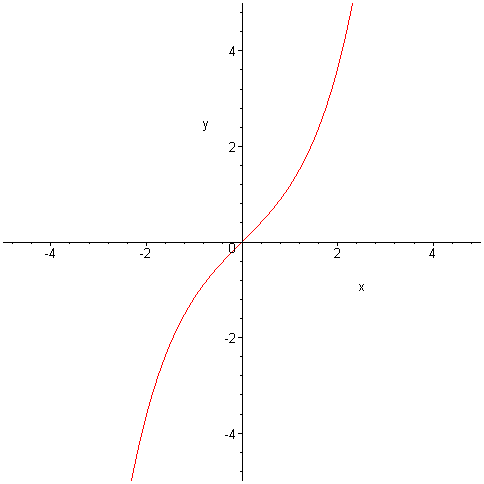
y = sinhx (sinh - czytamy sinus hiperboliczny)

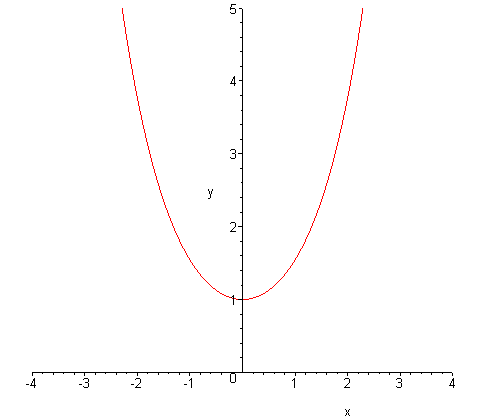
y = coshx (cosh - czytamy cosinus hiperboliczny)

y = tghx
tghx = sinhx/coshx

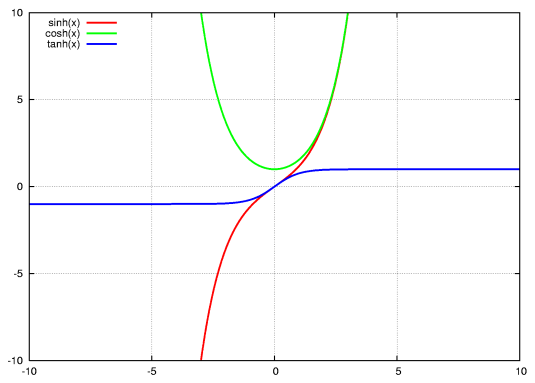
y = ctghx
tghx = 1/tghx

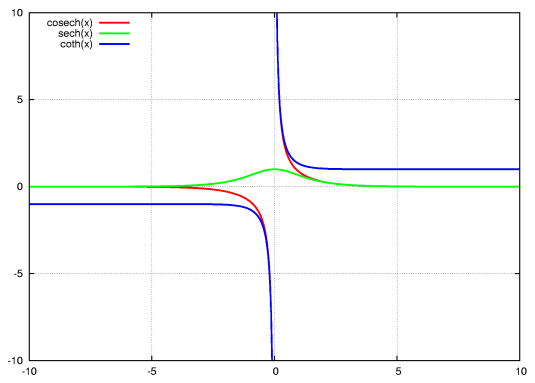
Funkcje równowartościowe:
Definicja:
(Funkcja ƒ jest różnowartościowa na zbiór A⊂D_ƒ)⇔(∀x_x1,x2∈A x₁≠x₂⇒ƒ(x₁)≠ƒ(x₂)

Twierdzenie:
(Funkcja ƒ jest różnowartościowa na zbiór A⊂D_ƒ)⇔(∀x_x1,x2∈A ƒ(x₁) = ƒ(x₂)⇒x₁ = x₂

Przyklady funkcji różnowartościowej w dziedzienie funkcji:

Przyklady funkcji które nie są różnowartościowe w dziedzienie funkcji:

Definicja:
Niech ƒ:X-na->Y będzie równowartościowa funkcja odwrotna do ƒ nazywamy funkcje:
ƒ^-1:Y-na->X określona przez warunek, ƒ^-1(y) = x⇔y = ƒ(x), gdzie y∈Y, x∈X

Uwaga
Oczywiście funkcja trygonometryczne nie są różnowartościowe.

Funkcje cyklometryczne (kołowe):
y = arc sinx (ARC SIN - czytamy arkus sinus)
jest to funkcja odwrotna do funkcji:
y = sinx, x∈<-π/2;π/2>

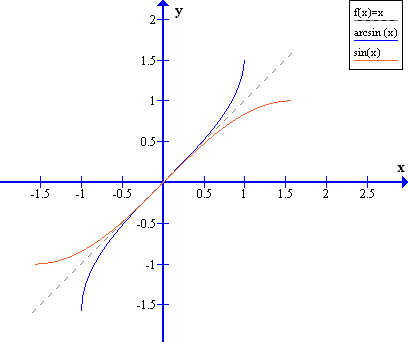
y = arc cosx - jest to funkcja odwrotna do y = cosx, x∈<0,x>

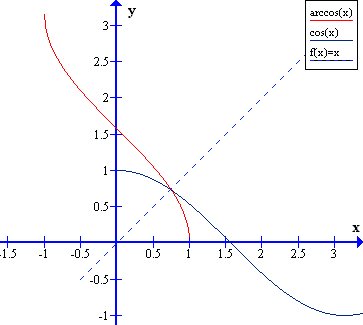
y = arc tgx - jest to funkcja odwrotna do y = tgx, x∈<-π/2,π/2>

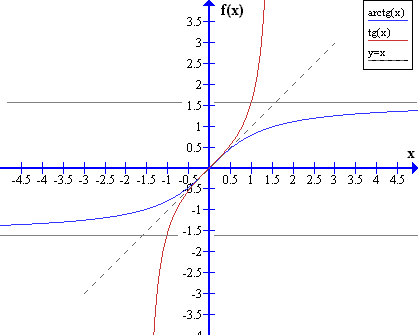
y = arc ctgx - jest to funkcja odwrotna do y = ctgx, x∈<0,π>
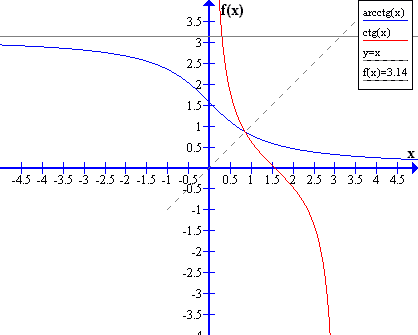